13. SciPy埃尔米特插值
埃尔米特插值是另一类插值问题,这类插值在给定的节点处,不但要求插值多项式的函数值与原函数值相同。同时还要求在节点处,插值多项式的一阶直至指定阶的导数值,也与被插函数的相应阶导数值相等,这样的插值称为埃尔米特($Hermite$)插值。
13.1 Hermite插值基本原理
$Hermite$插值在不同的节点,提出的差值条件个数可以不同,若在某节点$x_i$,要求插值函数多项式的函数值,一阶导数值,直至$\;m_i - 1\;$阶导数值均与被插函数的函数值相同及相应的导数值相等。我们称为重插值点节,因此,$Hermite$插值应给出两组数,一组为插值点{$\;x_i, \; i \in [0, n]\;$}节点,另一组为相应的重数标号{$m_i, \; i \in [0, n]$}。
对于$f(x)$在$[a, b]$上存在$n + 1$个互异点即$x_i$有$a \leq x_0 < x_1 < \cdots < x_n \leq b$,有$y_j = f(x_j)$, $m_j = f'(x_j)$对于$j$取值于$0,1,2,\cdots,n$,求插值多项式$H(x)$满足: $$H(x_j) = y_j,\; H'(x_j) = m_j, (j=0,1,2,\cdots,n)$$ 这里共需要$2n+2$个插值条件可以唯一确定一个$2n + 1$的多项式$H_{2n+1} = H(x)$,其形式为: $$ H_{2n + 1} = a_0 + a_1x+\cdots+a_{2n + 1}x^{2n + 1} $$ 先求出$\;2n+2\;$个插值基函数$\;\alpha_j(x)\;$和$\;\beta_j(x)\;$此处$\;j\;$取值$\;0,1,\cdots,n\;$,每个基函数都是$\;2n+1\;$次多项式,且满足: $$ \alpha_j(x_k)=\delta_{jk} = 0, \quad j\neq k\quad \alpha'_j(x_k) = 0 $$
$$ \alpha_j(x_k)=\delta_{jk} =1, \quad j = k\quad \alpha'_j(x_k) = 0 $$
$$ \beta_j(x_k) = 0, \quad \beta_j{'}(x_k) = \delta_{jk} $$
$$ j,k = 0,1,2,\cdots,n $$
此时,$H(x)$可以改写为: $$ H_{2n + 1}(x) = \sum_{j = 0}^{n}(y_j\alpha_j(x) + m_j\beta_j(x)) $$ 接下来求解这些插值基函数$\;\alpha_j(x)\;$和$\;\beta_j(x)\;$,利用朗日插值基函数$\;P_j(x)\;$,令: $$ \alpha_j(x) = (ax+b)P_j^2(x) $$ 有: $$ \alpha_j(x_j) = (ax_j+b)P_j^2(x_j) = 1 $$
$$ P_j(x_j) = 1 $$
对$\;\alpha_j(x)\;$求导得到$\;\alpha'_j(x)\;$即: $$ \alpha'_j(x) = aP_j^2(x_j) + 2(ax_j + b)P_j(x_j)P'_j(x_j) = 0 $$ 即: $$ a + 2(ax_j + b)P'_j(x_j) = 0 $$ 整理以上两式得到: $$ ax_j + b = 1 $$
$$ a + 2P'_j(x_j) = 0 $$
解之得: $$ a = -2P'_j(x_j) $$
$$ b = 1 + 2x_jP'_j(x_j) $$
已知 $$ P_j(x) = \prod_{i =0,i \neq j}^{n}\frac{x - x_i}{x_j - x_i} $$ 求导可得: $$ P_j^{'}(x_j) = \frac{1}{x_j - x_0}\times \frac{x_j - x_1}{x_j - x_1}\times \cdots\times \frac{x_j - x_n}{x_j - x_n} + \cdots + \frac{x_j - x_0}{x_j - x_0}\times \cdots \times \frac{x_j - x_{n-1}}{x_j - x_{n-1}}\times \frac{1}{x_j - x_n} =\sum_{i =0,i \neq j}^{n}\frac{1}{x_j - x_i} $$ 将$a = -2P_j^{'}(x_j)$和$b = 1 + 2x_jP_j^{'}(x_j)$代入公式$\;\alpha_j(x) = (ax+b)P_j^2(x)\;$得: $$ a_j(x) = (1-2(x - x_j)\sum_{i =0,i \neq j}^{n}\frac{1}{x_j - x_i})P_j^2(x) $$ 同理,$\beta_j(x)$为: $$ \beta_j(x) = (x - x_j)P_j^2(x) $$
13.2 Hermite插值计算
下面以经过$f(x) = x^3 + 1$的点(0,1)、(1,2)和导数$f'(0)=0$、$f'(1)=3$来求$Hermite$插值多项式。
这里有$x_0 =0, x_1 = 1, y_0 = 1, y_1 = 2$便可求得$\alpha_j(x)$和$\beta_j(x)$了。
首先计算$P_j(x)$: $$ P_0(x) = \frac{x - x_1}{x_0 - x_1} = \frac{x-1}{0-1} = 1-x $$
$$ P_1(x) = \frac{x - x_0}{x_1 - x_0} = \frac{x-0}{1-0} = x $$
接着计算$\alpha_j(x)$: $$ \alpha_0 = (1 - 2(x -0)\frac{1}{0-1})(1-x)^2 = (1+2x)(1-x)^2= 1-3x^2 + 2x^3 $$
$$ \alpha_1 = (1-2(x - 1)\frac{1}{1-0})x^2 = 3x^2-2x^3 $$
计算$\beta_j(x)$: $$ \beta_0(x) = (x - 0)(1-x)^2= x - 2x^2 + x^3 $$
$$ \beta_1 = (x - 1)x^2 = x^3 - x^2 $$
计算$H_{2n + 1}(x)$: $$ H_3(x) = \sum_{j = 0}^{1}(y_j\alpha_j(x) + m_j\beta_j(x)) = y_0\alpha_0(x) + m_0\beta_0(x)+y_1\alpha_1(x) + m_1\beta_1(x) $$ 代入上边求得的各值: $$ H_3(x) = 1\times(1-3x^2 + 2x^3) +0\times(x-2x^2+x^3) + 2\times(3x^2 -2x^3) + 3\times(x^3 - x^2) = x^3 + 1 $$ 即最后求得: $$ H_3(x) = x^3 + 1 $$ 与之前的$f(x)$表达式一模一样!
13.3 Hermite插值编程
SciPy里的Hermite插值实现函数是scipy.interpolate模块下的KroghInterpolator函数,其形参$x$和$y$必须同等长度,可以给出若干个坐标点作为形参,也可以给出每个$x_i$对应的$y_i$和导数。
13.3.1 坐标点作为形参
下面的程序代码是用四个坐标点作为函数的参数求得插值。KroghInterpolator函数要求$x_i$是递增序列。
from scipy.interpolate import KroghInterpolator
import numpy as np
import numpy as np, matplotlib.pyplot as plt
x = np.linspace(-5, 5, 100)
nodes = np.array([0,1,2,3])
def f(x):
return x**3 + 1
xi = np.array([0,1,2,3])
yi = np.array([1,2,9,28])
interpolant = KroghInterpolator(xi, yi)
plt.figure()
plt.subplot(121)
plt.plot(x, interpolant(x), 'b--',label='Hermite Interpolation')
plt.plot(nodes, f(nodes), 'ro', label='nodes')
plt.legend(loc=9)
plt.xlim(-10.5, 10.5)
plt.title('$f(x) = x^3 + 1$')
plt.subplot(122)
plt.plot(x, f(x), 'g--', label='orginal')
plt.plot(xi, f(xi), 'ro', label='nodes')
plt.legend(loc=9)
plt.title('$f(x) = x^3 + 1$')
plt.xlim(-10.5, 10.5)
plt.show()
程序执行结果如下:
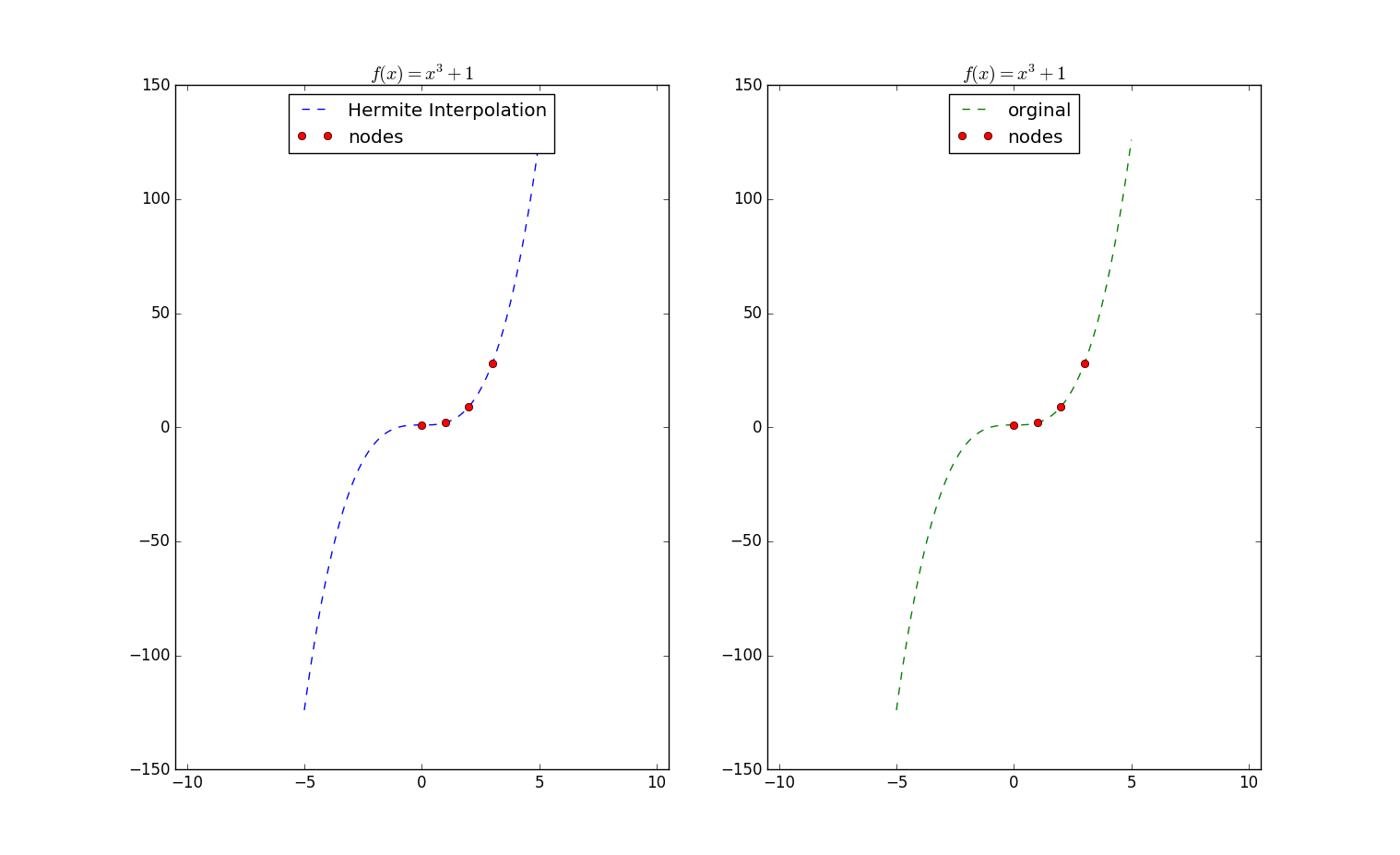
13.3.2 坐标和导数作为形参
由于KroghInterpolator要求$x$是递增序列,所以形参$x$里会多次出项某一个x轴坐标$x_i$,如果$x$里有多个同样的$x_i$,那么第二个参数$y$对应值分别为$x_i$的$f(x_i)$值、$f'(x_i)$一阶导数值、$f''(x_i)$二阶导数值$\cdots$$f^{(n)}(x_i)$n阶导数值。
from scipy.interpolate import KroghInterpolator
import numpy as np
import numpy as np, matplotlib.pyplot as plt
x = np.linspace(-5, 5, 100)
nodes = np.array([0,1])
def f(x):
return x**3 + 1
xi = np.array([0,0,1,1])
yi = np.array([1,0,2,3])
interpolant = KroghInterpolator(xi, yi)
plt.figure()
plt.subplot(121)
plt.plot(x, interpolant(x), 'r--',label='Hermite Interpolation')
plt.plot(xi, yi, 'go', label='nodes', markersize=8)
plt.legend(loc=9)
plt.xlim(-10.5, 10.5)
plt.title('$f(x) = x^3 + 1$')
plt.subplot(122)
plt.plot(x, f(x), 'b--', label='orginal')
plt.plot(xi, f(xi), 'go', label='nodes', markersize=8)
plt.legend(loc=9)
plt.xlim(-10.5, 10.5)
plt.title('$f(x) = x^3 + 1$')
plt.show()
程序执行结果:
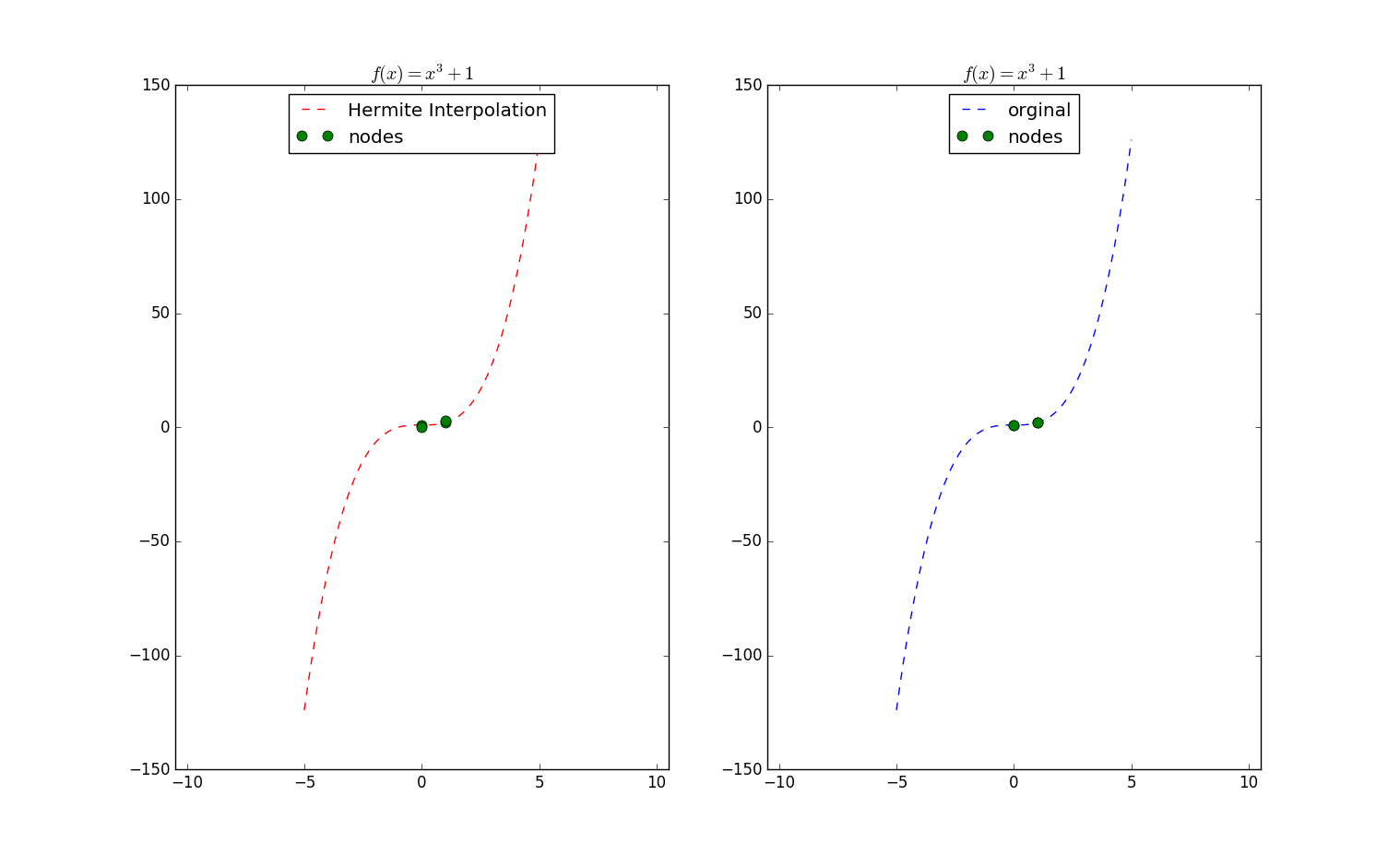
需要说明的函数的形参$xi$和$yi$:
xi = np.array([0,0,1,1])
yi = np.array([1,0,2,3])
在$xi$里有两个坐标$x_0= 0$和$x_1 = 1$,在$yi$里1是$f(0)$、0是$f'(0)$导数值、2是$f(1)$的计算值、3则是$f'(1)$的导数值。