8. SciPy范德蒙矩阵多项式逼近
本章基于范德蒙(德)Vandermonde矩阵求若干点的多项式表达式。
8.1 范德蒙矩阵
范德蒙矩阵行数为m,列数为n,矩阵具有最大的秩min(m, n),其形式如下所示:
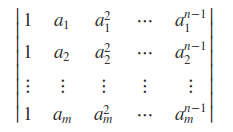
在numpyPy模块下可以利用polynomial子模块的polynomial.polyvander构造出范德蒙矩阵来或者用scipy的vander也可构造出范德蒙矩阵来。
8.2 多项式逼近与范德蒙
范德蒙矩阵和多项式有啥关系呢?假设现在有4个点(1,1),(2,3),(3,5),(4,4)有没有一个x的3次多项式刚好经过这四个点呢?即$f(x) = c_0x^0 + c_1x^1 + c_2x^2 + c_3x^3$,如果能得到$(c_0,c_1,c_2,c_3)$这个四个系数就能确定$f(x)$了。由于假设这四个点经过了$f(x)$,那么便有:
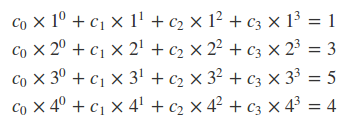
写成矩阵表示形式如下:
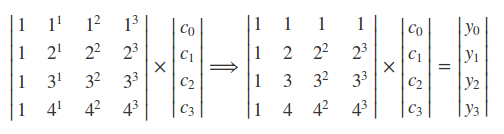
上边$4\times4$的矩阵不就是范德蒙矩阵么?形如$Ax=y$的且知道A和y就可以用solve函数来求得x的值,这里的x就是$f(x) = c_0x^0 + c_1x^1 + c_2x^2 + c_3x^3$方程里的系数$c_i$构成的向量$(c_0,c_1,c_2,c_3)$。而scipy.vander刚好可以基于四个点的x坐标$(1,2,3,4)$构造出这个$4\times4的矩阵$
import scipy
import numpy as np
import numpy.polynomial.polynomial as npp
x = np.array([1,2,3,4])
A = scipy.vander(x,increasing=True)
print A,"#A"
A = npp.polyvander(x, 3)
print A,"#A"
程序执行结果:
[[ 1 1 1 1]
[ 1 2 4 8]
[ 1 3 9 27]
[ 1 4 16 64]] #A
[[ 1. 1. 1. 1.]
[ 1. 2. 4. 8.]
[ 1. 3. 9. 27.]
[ 1. 4. 16. 64.]] #A
8.3 范德蒙矩阵多项式逼近
好回到原问题求$f(x)$的各个系数就可最终知道$f(x)$了:
1). 首先给出四个点的x和y坐标
import numpy as np
x = np.array([1, 2, 3, 4])
y = np.array([1, 3, 5, 4])
2).用$x$构造上边那个$4\times4$矩阵,可以用scipy.vander函数构造。
import scipy
A = scipy.vander(x,increasing=True)
print A,"#scipy"
或者用numpy的模块来构造也行,
import numpy.polynomial.polynomial as npp
A = npp.polyvander(x, 3)
print A,"#A"
3). 方程$Ax=y$有了$A$和$y$求x(这里是求c系数)可以用solve函数求解。
c = np.linalg.solve(A, y)
print c
c即是$f(x) = c_0x^0 + c_1x^1 + c_2x^2 + c_3x^3$方程里的各个系数$c_i$,这样方程就找到了。
8.4 SciPy多项式逼近程序
基于范德蒙矩阵多项式逼近完整的程序如下所示:
import numpy.polynomial.polynomial as npp
import numpy as np
import scipy
x = np.array([1, 2, 3, 4])
y = np.array([1, 3, 5, 4])
A = npp.polyvander(x, 3)
print A,"#numpy"
A = scipy.vander(x,increasing=True)
print A,"#scipy"
c = np.linalg.solve(A, y)
print c,"#c"
x = np.linspace(1,50, 50)
y = c[0] + c[1] * x + c[2]*(x**2) + c[3]*(x ** 3)
import matplotlib.pyplot as plt
plt.plot(x[:4], y[:4],'go')
plt.xlim(-1,6)
plt.ylim(-1,6)
plt.show()
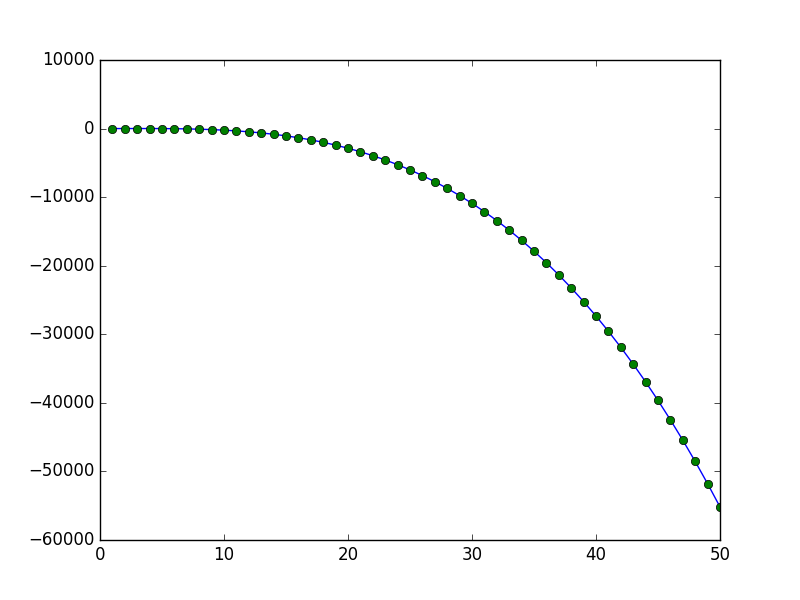
plt.plot(x, y)
plt.plot(x, y,'go')
plt.show()
程序执行结果:
[[ 1. 1. 1. 1.]
[ 1. 2. 4. 8.]
[ 1. 3. 9. 27.]
[ 1. 4. 16. 64.]] #numpy
[[ 1 1 1 1]
[ 1 2 4 8]
[ 1 3 9 27]
[ 1 4 16 64]] #scipy
[ 2. -3.5 3. -0.5]#c
从c的输出[ 2. -3.5 3. -0.5]得知方程为:
$f(x) = c_0x^0 + c_1x^1 + c_2x^2 + c_3x^3 =2\times x^0 -3.5\times x^1 + 3\times x^2 -0.5\times x^3 =2-3.5 x + 3x^2 -0.5 x^3$
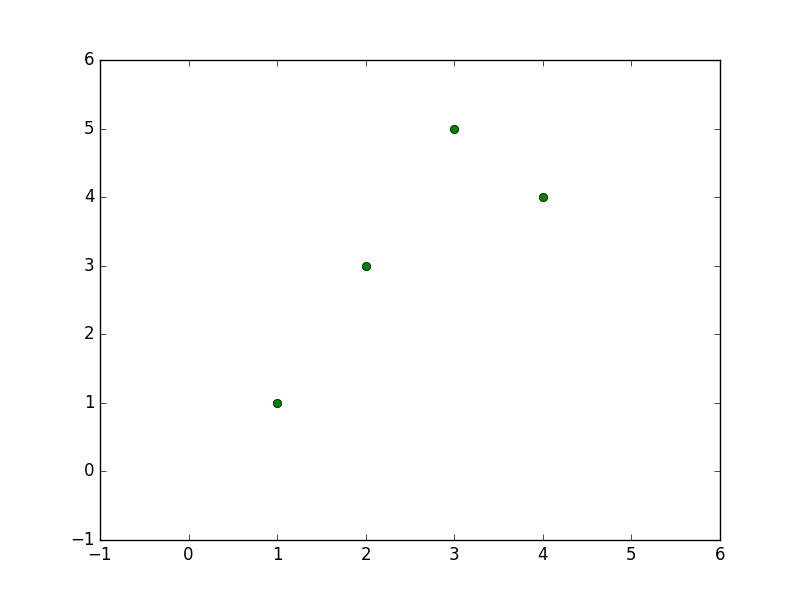
可视化输出(1,1)、(2,3)、(3,5)、(4, 4)四个点如下所示: